『白と黒のとびら』 第9章 「不毛な論争」まとめ ①
前半の山場である９章「不毛な論争」の内容が、一度読んだだけでは頭に入ってこなかったので、ここにまとめておく。
証明
①『規則』で表せる文はすべて『装置』で表すことができる。
②『装置』で表せる文はすべて『規則』で表すことができる。
「装置」の定義（p.174）
・白と黒の扉のついたいくつかの部屋からなる遺跡であること。
・一定の条件に従って、筒の中身が変化すること。
・どの部屋でどの扉を選ぶか、また筒の中身がどのような状態にあるかによって、移動先の部屋が決まること。
・筒の中身は、後から入れたものほど先に出され、先に入れられたものは後から出されること。
「規則」の定義（p.174）
・「→」の左側に「いずれ何らかの文字列に置き換えられる記号」を一つだけもつものがあること。
・「→」の右側に、文字列か、「いずれ何らかの文字列に置き換えられる記号」か、あるいはその両方をもつものがあること。
予備知識
第一古代クフ語（一つ以上の○の後に、同じ数の●が連続する文字列のみを文とみなす言語（p.78）。この言語の文の例：○●、○○○●●●、○○○○○○●●●●●●。）
以下で、この言語のあらゆる文が、規則と装置のいずれによっても表現できることを示す。
★（１）と（２）の規則によって、第一古代クフ語のあらゆる文は表現可能。
・最初に（２）を使うと○●という第一古代クフ語の最短の文が作れる。
・最初に（１）を使うと、Sが残るため、次に（１）か（２）を使用する必要がある。ここでもし（２）を使うと、○○●●という二番目に短い文が作れる。（１）を使うと、また（１）か（２）を選ぶ地点に戻る。（１）を繰り返すことで文を無限に長くしていけるため、規則（１）（２）で第一古代クフ語のすべての文が表現できる。
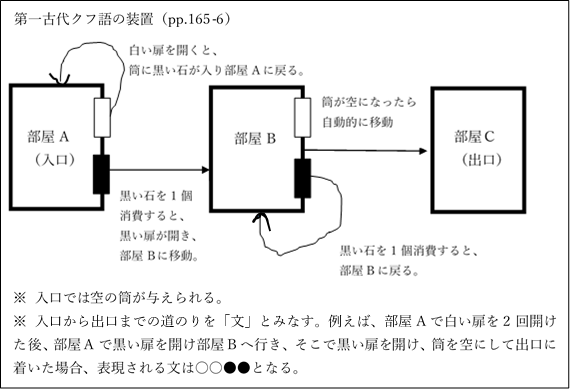
★この装置によって、第一古代クフ語のあらゆる文は表現可能。
・出口へ行くためには部屋Bに行く必要がある。だが、部屋Bへ行くためには黒い石が必要であるため、少なくとも1回は部屋Aで白い扉を開かなければならない。そこで部屋Aで白い扉を開くと、黒い石が手に入る。ここで黒い扉を開くと部屋Bへ移動し、黒い石は取り去られる。もしここで筒が空ならば、出口に着く。これが最短（文○●）。
・もし、部屋Aで二回以上白い扉を開けると、その分だけ黒い石が溜まる。筒が空でなければ外に出られないため、二回目以降に獲った黒い石は部屋Bの黒い扉を同じ回数だけ開けることで消費される。従って、部屋Aでの二回目以降の白い扉を開けた回数と、部屋Bで黒い扉を開けた回数は一致する。
・部屋Aで白い扉は何度でも開くことができるため、第一古代クフ語のすべての文を表現することができる。
ひとまずの結論
・第一古代クフ語に限っていえば、あらゆる文は『規則』でも表現できるし、『装置』でも表現できる。
・証明したいのは、古代クフ語全体について、『規則』で表現できる文は『装置』でも表現できて、その逆も成り立つということ。言い換えれば、『規則』で表現できて『装置』で表現できない文（あるいはその逆）は存在しないことを示す。あと数ステップ必要みたいだ。
・［ひとつ思うこと］第一古代クフ語の文は無限個存在する。『規則』や『装置』は、第一古代クフ語のあらゆる（無限個の）文を表現できると言い切ってよいのだろうか。ある文について対応する『規則』や『装置』は示せる。が、それに尽きると言ってよいのか。もちろん直感的には分かるけども。南無―。続く。
何気に戦闘シーンもあって面白い。
